Model Predictive Control_Part 1

Everyday advancements in technology make many dreams more feasible, and one such dream is sustainable autonomous transportation. Autonomous transportation is already a reality in some transportation modes. Over the years, for example, we have seen the introduction of semi-autonomous and full-autonomous aerial vehicles, and in the recent decade, autonomous capabilities have been making their way into ground and marine vehicles, such as cars and vessels. But how do we achieve autonomy in these mechanical systems? Different branches of engineering are required to find a solution and one of them is control engineering. From the control science perspective, understanding the behavior of a system is essential to suggest a controller that enables autonomous operation. Among the various control schemes, Model Predictive Control (MPC) is a promising approach for this application.

Let’s see what MPC is and why it is important. MPC is an advanced control strategy that governs a system while satisfying a series of constraints. The target system can be an industrial process or a mechanical system, including chemical reaction processes, power plants, robotics, and more. MPC-based approaches have made remarkable progress in recent decades and have become valuable assets in both research and industry. The success of MPC can be attributed to its superior capacity to solve control problems in the time domain while handling a set of constraints and limits which root either in physical properties of the system or the required conditions.

Some important features of the MPC scheme are as follows:

• A limited amount of information or knowledge regarding control systems is required to set up the scheme, making it easy for users to initialize and tune MPC controllers.
• MPC controllers are applicable to various types of systems, including systems with delay, single-input single-output, multi-input multi-output, and non-minimum phase systems, among others.
• Since MPC can handle constraints, it is an ideal solution for systems with restrictions.
• Ease of implementation.

The basic idea behind MPC is to make the future outputs of the system track specific values by determining the appropriate control signal through solving a constrained optimization problem over a finite horizon. Figure 1 illustrates the core notion of MPC [2]. In this figure, y is the output of the system in respect to previous inputs U, ŷ is the predicted output and u is the future control actions.

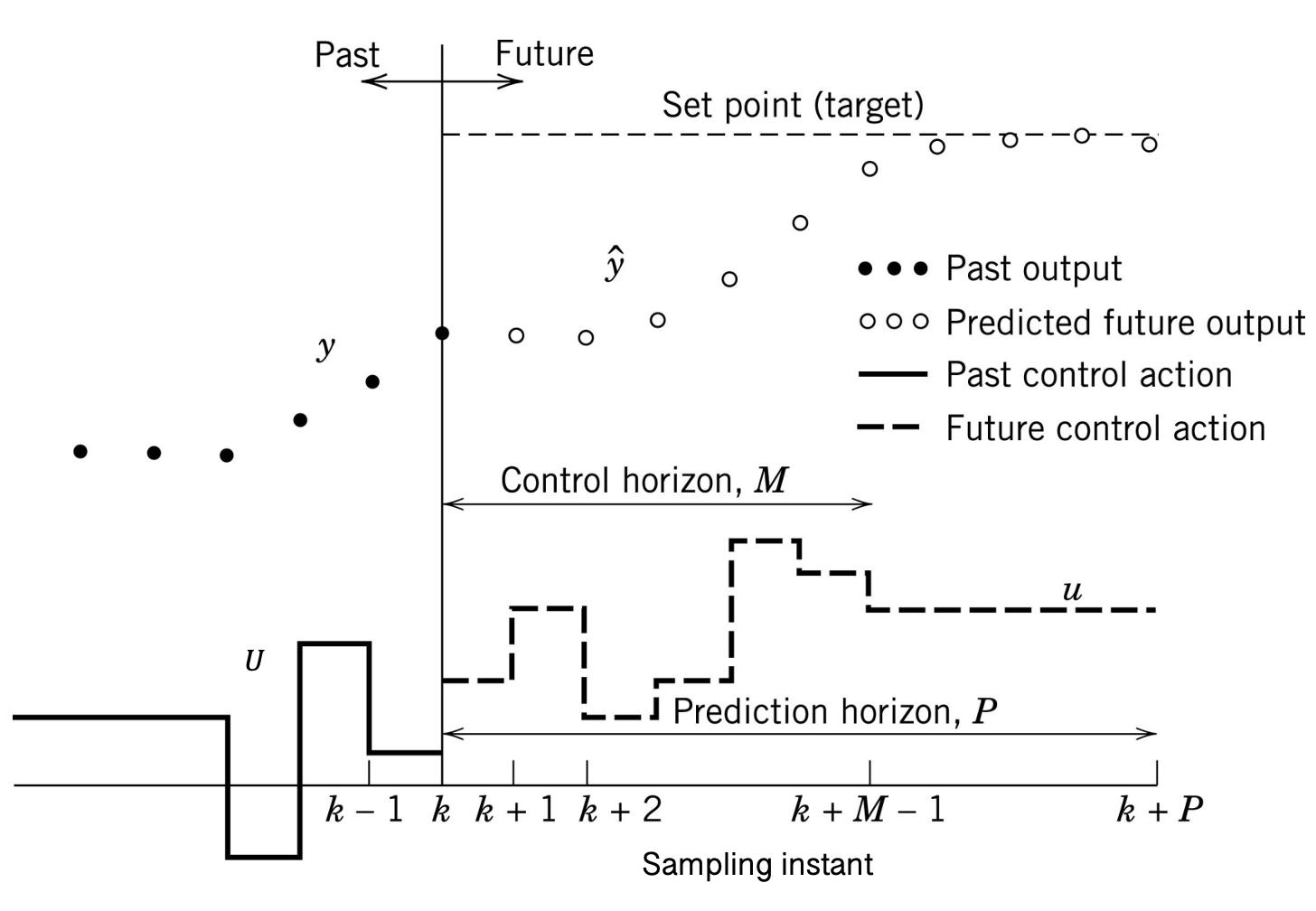
Figure 1: Basic concept for Model Predictive Control [2].

Depending on the application and how the system is modeled, various algorithms have been presented to implement MPC. Dynamic Matrix Control (DMC), Model Algorithmic Control (MAC), Predictive Functional Control (PFC), Generalized Predictive Control (GPC) are among the most well-known algorithms for linear systems.

Dynamic Matrix Control
Based on the system’s step response, this algorithm determines the necessary changes in the control signal to minimize a running cost while preserving the input/output constraints. The proposed cost function is usually based on the error from a set point.

Model Algorithmic Control
This algorithm is similar to DMC but with this difference that it uses the impulse response of the system instead of the step response in DMC method.

Predictive Functional Control
This algorithm can be noted as the bridge between proportional integral derivative (PID) controllers and complex MPC schemes and it is one of the most widely used predictive control techniques in the industry. The feature input is chosen in respect to the degrees of freedom, and through minimizing a cost function this method will choose the decision variables.

Generalized Predictive Control
This strategy uses the system transformation function model in the frequency domain to predict the future behavior of the plant and benefits from a wider application than other algorithms.

To be continued.

An article by AmirReza Haqshenas Mojaveri

References
[1] Camacho, E. F., & Alba, C. B. (2013). Model predictive control. Springer science & business media.
[2] Seborg, D. E., Edgar, T. F., Mellichamp, D. A., & Doyle III, F. J. (2016). Process dynamics and control. John Wiley & Sons.